Caída libre y lanzamiento vertical

De entre todos los movimientos rectilíneos aceleradosque se dan en la naturaleza, existen dos de particular interés: la caída libre y el lanzamiento vertical. Ambos se rigen por las ecuaciones propias de los movimientos rectilíneos acelerados:

y=y0+v0t+12at2

v=v0+a⋅t

a=cte

Lanzamiento Vertical

En el lanzamiento vertical un objeto es lanzado verticalmente hacia arriba o hacia abajo desde cierta altura H despreciando cualquier tipo de rozamiento con el aire o cualquier otro obstáculo. Se trata de un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en el que la aceleración coincide con el valor de la gravedad. En la superficie de la Tierra, la aceleración de la gravedad se puede considerar constante, dirigida hacia abajo, se designa por la letra g y su valor es de 9.8 m/s2.

Para estudiar el movimiento de lanzamiento vertical normalmente utilizaremos un sistema de referencia cuyo origen de coordenadas se encuentra en el pie de la vertical del punto desde el que lanzamos el cuerpo y consideraremos el sentido positivo del eje y apuntando hacia arriba, tal y como puede verse en la figura:

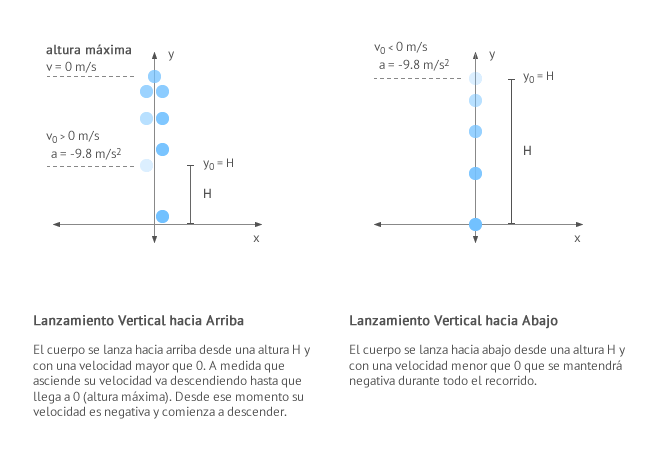
El lanzamiento vertical es un movimiento rectilíneo uniformemente acelerado  o movimiento rectilíneo uniformemente variado en el que se lanza un cuerpo verticalmente con cierta velocidad inicial desde cierta altura y no encuentra resistencia alguna en su camino. Podemos distinguir dos casos según el sistema de referencia considerado:

• Lanzamos el cuerpo hacia arriba y por tanto velocidad inicial positiva (v0>0). En este caso las ecuaciones del lanzamiento vertical hacia arriba son:
  
  

  y=H+v0t−12gt2
  
  

  v=v0−g⋅t
  
  

  a=−g
• Lanzamos el cuerpo hacia abajo y por tanto velocidad inicial negativa (v0<0). En este caso las ecuaciones del lanzamiento vertical hacia abajo son:
  
  

  y=H−v0t−12gt2
  
  

  v=−v0−g⋅t
  
  

  a=−g

Donde:

• y: La posición final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro (m)
• v, v0: La velocidad final e inicial del cuerpo respectivamente. Su unidad en el Sistema Internacional (S.I.) es el metro  (m/s)
• a: La aceleración del cuerpo durante el movimiento. Su unidad en el Sistema Internacional (S.I.) es el metro (m/s).
• t: Intervalo de tiempo durante el cual se produce el movimiento. Su unidad en el Sistema Internacional (S.I.) es el segundo (s)
• H: La altura desde la que se lanza el cuerpo. Se trata de una medida de longitud y por tanto se mide en metros.
• g: El valor de la aceleración de la gravedad que, en la superficie terrestre puede considerarse igual a 9.8 m/s2

Fuente: Fisicalab.com

Problemas resuelto online

Phet Simulation (coloca el cañón a 90° para que sea caída libre)